转载至：

一、哈夫曼树的定义

　　(1)简单路径长度

　　所谓树的简单路径长度，是指从树的根结点到每个结点的路径长度之和。　　完全二叉树是简单路径长度最小的二叉树

　　(2)加权路径长度

　　　　所谓树的加权路径长度，是指树中所有带权(非0)叶节点的加权路径长度之和。

　　　　如下图所示，不同的树结构，加权路径长度也不一样。

　　　　

　　　　1：WPL=1*4+2*4+3*3+4*2+5*1=34  (加粗为路径长度)

　　　　2：WPL=5*4+4*4+3*3+2*2+1*1=50

　　　　3：WPL=1*3+2*3+3*2+4*2+5*2=33

　　（3）哈夫曼树的定义

　　　　哈夫曼树又称最优二叉树。哈夫曼树是指具有相同结点的树中，加权路径长度最小的二叉树。

二、哈夫曼树的构造过程

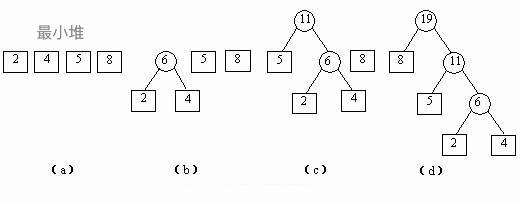
　　哈夫曼树的构造过程需要借助最小堆算法。

　　如下图所示，首先将原始数据构造出一个最小堆，然后每次从堆中选取值最小两个节点，计算他们的权重之和，作为一个新结点的值，然后插入到最小堆中，直到所有数据结点都构造完毕，成为一个最大堆。

　　

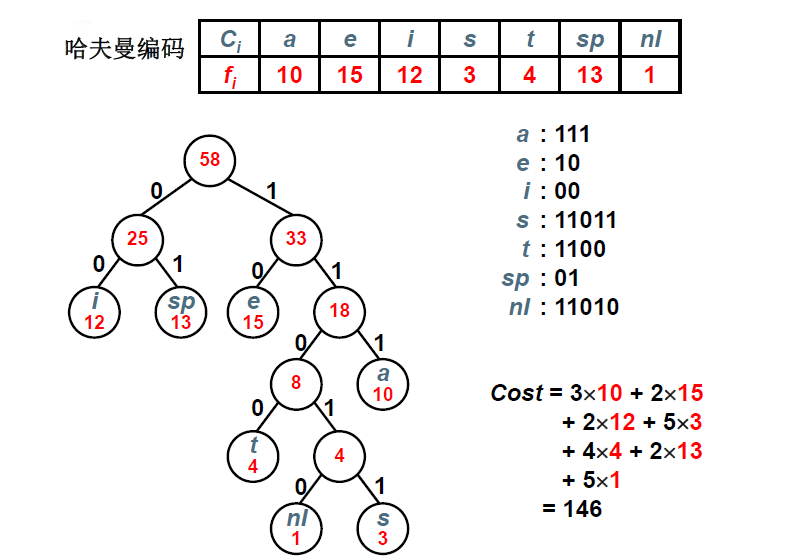
三、哈夫曼树的作用(哈夫曼编码)

　　　　哈夫曼编码是一种编码方式，是一种用于无损数据压缩的权编码算法。编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。